Linear Regression 이란?

Linear Regression 이란 무엇인가?

Linear Regression 에 대해 사전적인 의미를 찾아 보면 선형 회귀 라고 표현을 한다. 위키 백과에서는 다음과 같이 표현한다.

선현 회귀는 종속 변수 y 와 한 개 이상의 독립 변수 x와의 선형 상관 관계를 모델링하는 회귀분석 기법이다. 한 개의 설명 변수에 기반하는 경우는 단순 선형 회귀, 둘 이상의 설명 변수에 기반한 경우에는 다중 선형 회귀라고 한다.

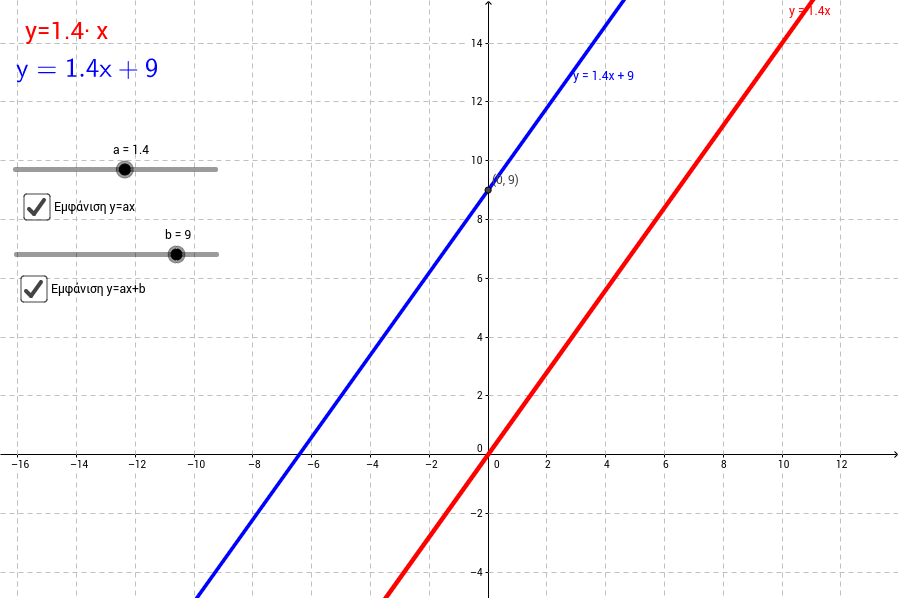
쉽게 이야기 해서 주어진 데이터가 어떤 함수로부터 생성됐는가를 알아보는 ‘함수 관계’ 를 추측하는 것이다. 여기에서 나오는 Hypothesis(가설)은 이러한 Linear Regression 그래프가 되며 방정식으로는 다음과 같이 표현이 가능하다.

H(x) = Wx + b

이러한 방정식은 아마도 아래와 같은 직선 형태의 그래프를 그릴 것이다.

Cost function

그렇다면 어떠한 그래프가 우리가 원하는 가설에 가까운 값일까? 아래의 이미지를 보면 그래프(가설)와 점(데이터) 사이에 거리가 멀면 가설이 잘못되었다는 것이고, 가까울수록 가설이 일치한다는 의미가 된다.

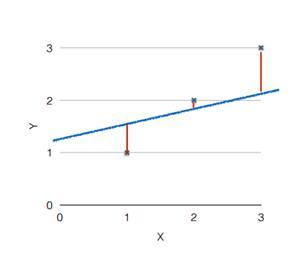
이러한 거리를 측정하는 것을 Cost function 혹은 Loss function 이라고 표현한다. 이러한 Cost function 을 계산하는 법으로는 (H(x) - y)² 와 같이 가설과 실제 데이터의 차의 제곱을 계산하는 것이다. 여기에서 제곱을 해주는 이유는 해당 값이 음수가 될 수도, 양수가 될 수도 있어 정확한 지표 비교가 힘들고, 또한 제곱을 함으로써 차이가 크면 그 값의 차이가 더 커져 비교하기가 쉬울 것 이다.

다시 위에 있는 그래프와 같이 3개의 실제 데이터를 비교한다면 다음과 같다.

((H(x¹) - y¹)² + (H(x²) - y²)² + (H(x³) - y³)²) / 3

3개의 실제 데이터의 Cost function 을 모두 더한 후에, 갯수 3 만큼 나누어준다. 하지만 이 또한 데이터의 양이 많이진다고 하면 해당 수식으로는 해결하기가 힘들 것이다. 이런 경우에 일반적으로 다음과 같이 표현한다.

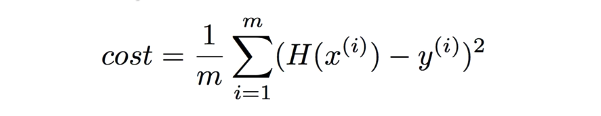
여기에서 m은 실제 데이터의 갯수를 나타낸다.