자료구조, 트리(Tree)
Tree 란 무엇인가?
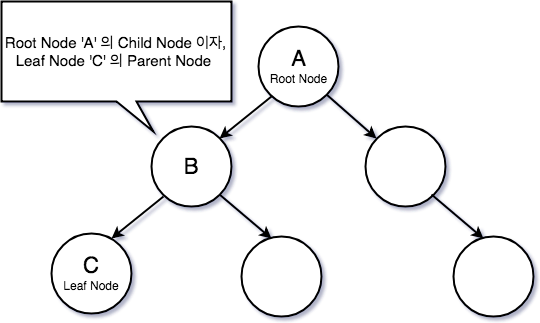
위키 백과에 따르면 트리 구조 란 그래프의 일종으로 여러 노드가 한 노드를 가리킬 수 없는 구조이다. 라고 표현을 하고 있다. 이 말을 조금 더 자세히 풀어 보면 노드가 하나 이상의 자식이 있는 경우를 Tree 라 하며, 임의의 노드에서 다른 어떠한 노드로의 경로가 하나 밖에 존재하지 않는 데이터의 구조를 가진 것을 트리 구조라고 부른다. 인터넷에 자료구조 트리 라고 치면 바로 나오는 데이터 구조의 형태가 아래와 같이 노출된다.

트리 구조 에서 최상위 노드 A 를 Root Node 라 표현한다. 노드 B는 Root Node 의 Child Node 이자, 노드 C 의 Parent Node 이다. 노드 C 와 같이 Child 노드가 없는 노드의 경우를 Leaf Node 라 부른다.
이진 트리 - Binary Tree
자료 구조 Tree 에 대해서 공부를 한다고 하면 대부분이 이진 트리 혹은 이진 탐색 트리에 대해서 공부를 할 정도로 많은 사람들이 관심을 가장 많이 보이는 트리 자료 구조이다. 이진 트리 같은 경우는 각각의 노드가 최대 2개의 자식 노드를 가질 수 있다. 3개의 자식 노드를 가지는 트리 구조로는 Ternary Tree 가 있지만, 해당 블로그에서는 이진 트리에 대해서만 다룬다. 혹시라도 관심 있는 사람은 개인적으로 찾아보는 것을 추천한다.
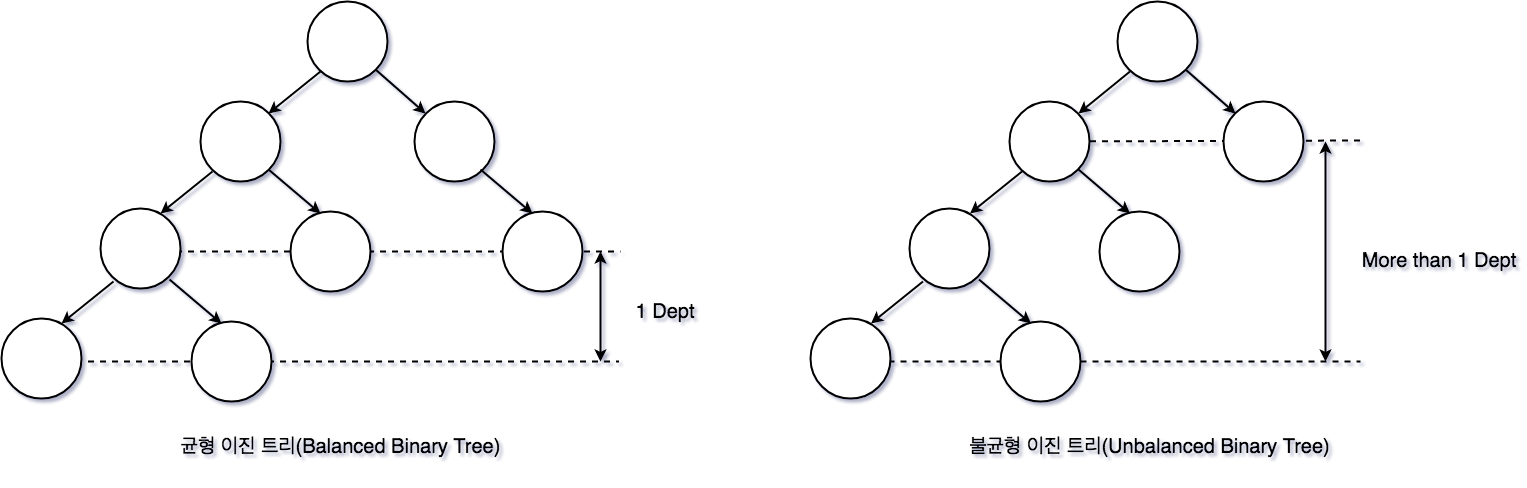
균형 이진 트리(Balanced Binary Tree) 와 불균형 이진 트리(Unbalanced Binary Tree)
균형 이진 트리(Balanced Binary Tree) 는 각자의 모든 노드가 가지는 Child Node 의 깊이가 1 이상 차이 나지 않는 이진 트리를 일컫는다.
이진 트리 모양에 따른 종류
모양에 따른 분류는 대표적으로 포화 이진 트리(Full Binary Tree), 완전 이진 트리(Complete Binary Tree) 그리고 포화 이진 트리(Perfect Binary Tree) 등 총 3가지로 나누어서 볼 수 있다.
포화 이진 트리(Full Binary Tree)
포화 이진 트리는 모든 노드가 자식 노드를 0개 혹은 2개를 갖는 구조를 말한다.
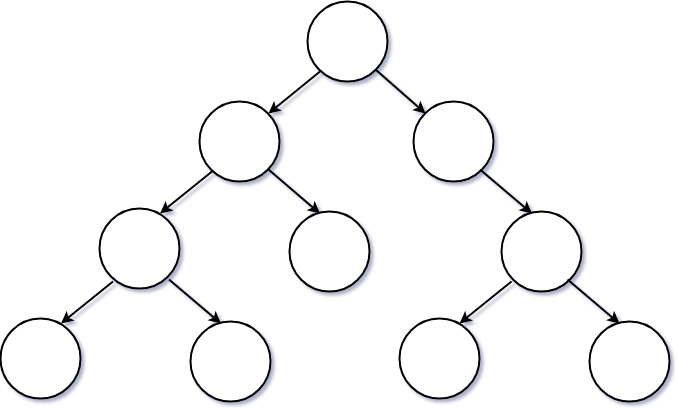
완전 이진 트리(Complete Binary Tree)
완전 이진 트리는 Leaf Node 를 제외하고 모든 노드가 2개의 자식 노드를 가지거나 마지막 노드는 가능한 가장 왼쪽에 있는 트리 구조를 말한다.
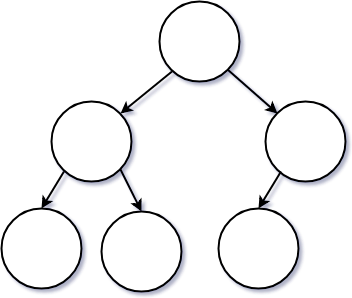
포화 이진 트리(Perfect Binary Tree)
완전 이진 트리와 조금 헷갈릴 수 있는 트리 구조로서, 모든 내부 노드가 두개의 자식 노드를 가지고, 깊이 역시 동일한 트리 구조를 말한다.
이진 탐색 트리(Binary Search Tree) 특징
이진 탐색 트리는 이진 트리 자료 구조로서 다음과 같은 특징을 가진다.
- 각 노드에는 값이 존재한다.
- 노드의 왼쪽에는 타겟 노드 보다 작은 값들로 이루어져 있다.
- 노드의 오른쪽에는 타겟 노드와 같은 값이거나 큰 값들로 이루어져 있다.
- 좌우 하위 트리는 다시 이진 탐색 트리 여야 한다.
이진 탐색 트리(Binary Search Tree) 구현
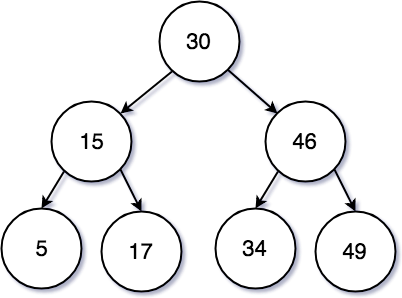
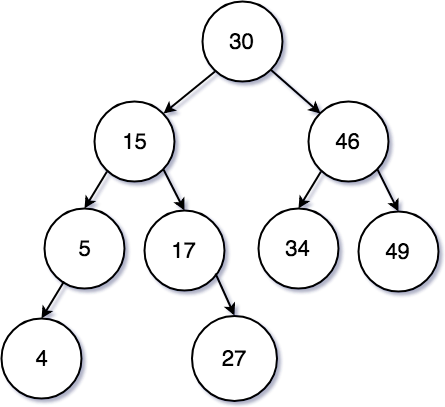
아래와 같은 데이터가 각각의 노드로 들어가 있다고 가정을 해보겠다.
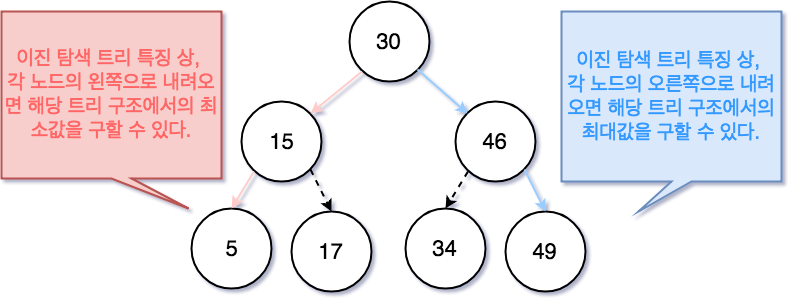
위에서 설명 했듯이, 노드의 왼쪽은 타겟 노드보다 작은 값이, 오른쪽으로는 타겟의 노드보다 큰 값이 있다. 이러한 특성을 이용하여 최소값과 최대값에 쉽게 접근할 수 있다. 아래의 사진과 같이 빨간 선을 따라 자식 노드의 왼쪽으로 이동하면 최소값 5 에 접근이 가능하고, 파랑선을 따라 자식 노드의 오른쪽으로 이동하면 최대값 49 에 접근할 수 있다.
그렇다면 이러한 트리에 노드를 추가하는 경우는 어떻게 될까?
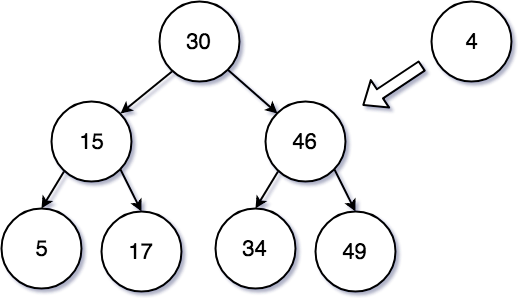
위에서의 규칙과 마찬가지의 규칙을 적용한다고 하면 쉽게 추가가 된다.
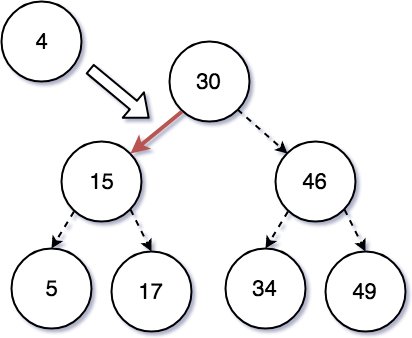
새로운 노드 ‘4’ 를 기존의 이진 탐색 트리에 삽입을 하려고 한다. 일단 노드 4는 루트 노드 30 보다는 작은 값이라 왼쪽으로 이동시킬 것이다. 루트 노드 30 왼쪽의 자식 노드로는 15 가 있다. 이진 탐색 트리의 특징 중에는 좌우 하위 트리는 다시 이진 탐색 트리여야 한다 라는 것이 있다. 그렇다면 루트 노드인 30 의 하위 자식 노드 15 로 이동했을 때도 마찬가지로 이진 탐색 트리의 규칙을 따라야 한다. 4는 15보다 작은 수 이기 때문에 왼쪽으로 이동한다.
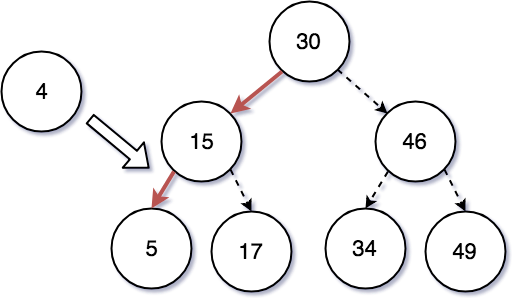
Leaf Node 에 해당하는 5 에 도달했을 때, 4 는 5 보다 작으므로 마찬가지로 왼쪽으로 이동된다. 그 후에는 하위에 더 이상 자식 노드가 없기 때문에 5 의 왼쪽 자식 노드로 추가된다.
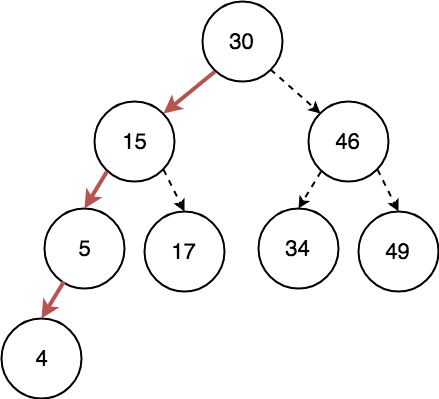
삭제에 대한 기능은 하위 Leaf Node 인 경우에는 큰 문제 없이 삭제 된다. 만약 Leaf Node 인 34 를 삭제 하려고 한다면 그냥 삭제를 해주면 된다.
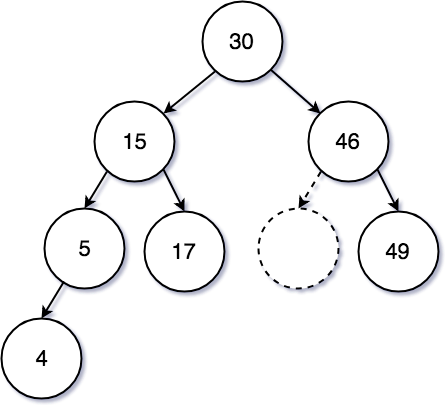
반대로 46과 같은 하위에 자식 노드가 있더라도 깊이가 1이 넘지 않은 경우는 왼쪽 자식 노드를 위로 올리면 된다.
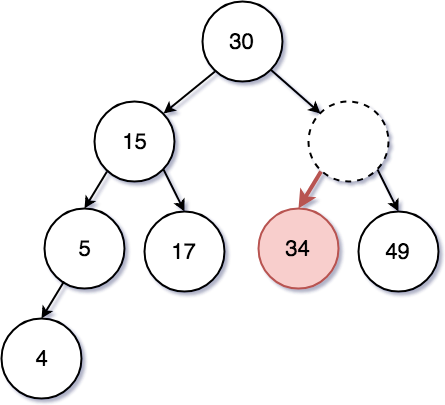
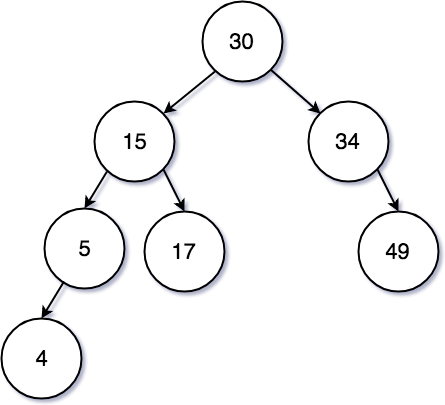
그렇다면 위와 같은 방법으로 삭제를 하되 조금더 복잡한 이진 탐색 트리의 구조는 어떠할까?
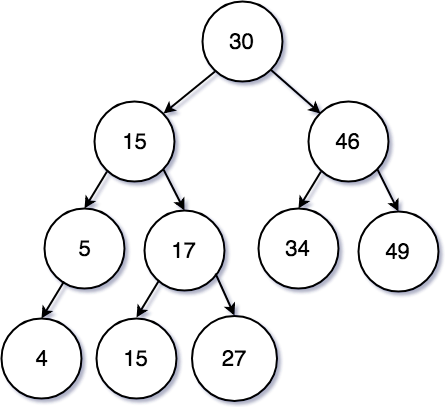
위와 같은 구조에서 만약 중간에 껴있는 15를 삭제할 경우는 다른 것보다는 더 복잡하다. 방법은 두가지가 있다. 첫번째는 15의 왼쪽 자식 노드 중 최대값을 위로 올리는 방법이고, 두번째는 오른쪽 자식 노드 중 최소값을 위로 올리는 방법이 있다. 아래의 예제에서는 오른쪽 자식 노드의 최소값을 올리는 방식으로 진행해보겠다.
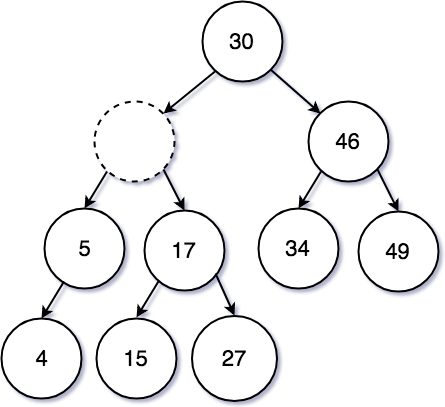
삭제된 15를 기준으로 오른쪽 노드를 살펴보면 17이 있다. 그리고 그 17 아래로 최소값 노드인 15가 있다. 이 값을 지원 타겟으로 이동시키면 된다.
이상으로 대략적인 이진 탐색 트리에 대해서 알아보았다.