하노이 탑 알고리즘

하노이 탑 알고리즘

하노의 탑 알고리즘은 많은 기업에서도 입사 문제로 많이 나올 정도로 유명한 알고리즘 중 하나이다. 아무런 지식 없이 바로 이 문제를 받는 다고 한다면 굉장히 주관적으로는 풀기가 불가능할 정도로 굉장히 어려운 문제이다. 하노이는 대표적인 재귀함수를 이용한 풀이 문제이다. 문제는 다음과 같다.

세 개의 기둥과 이 기동에 꽂을 수 있는 크기가 서로 다른 원판들이 있다. 퍼즐을 시작하기 전에는 한 기둥에 원판들이 큰 것에서부터 작은 것 순서대로 큰 원판이 아래로 작은 원판이 위로 순서대로 쌓여있다. 이 원판을 다른 원판으로 옮겨야 한다.

문제만 봤을 때는 자체가 어려워 보이지 않는다. 하지만 역시 쉽지 않게 다음과 같은 조건들이 붙는다.

1. 한 번에 하나의 원판만 옮길 수 있다.
2. 큰 원판이 작은 원판 위에 있어서는 안된다.
3. 1번에는 n개의 원판이 있고 이 n개의 원판을 3번 원판으로 최소 횟수로 옮겨야 한다.

위의 조건을 만족하면서 문제를 한번 풀어보기 전에 먼저 그림으로 대략적으로 확인을 해보면 어느 정도 길이 보인다.

그림으로 풀이하기

아래의 그림과 같이 1번 원반이 있을 경우에 옮기기가 쉽다.

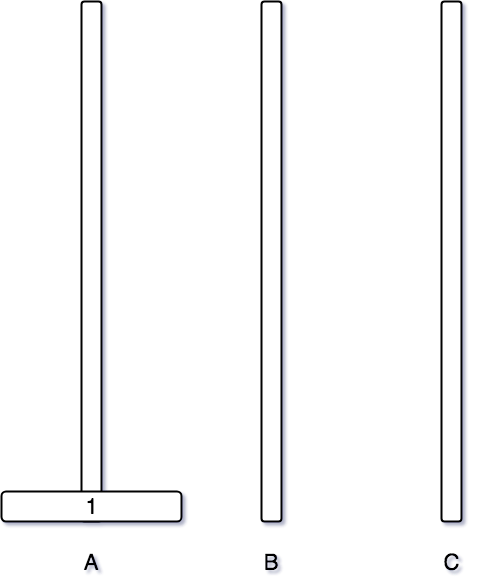
그냥 A 기둥에 있는 원판 1번을 옮기면 된다.

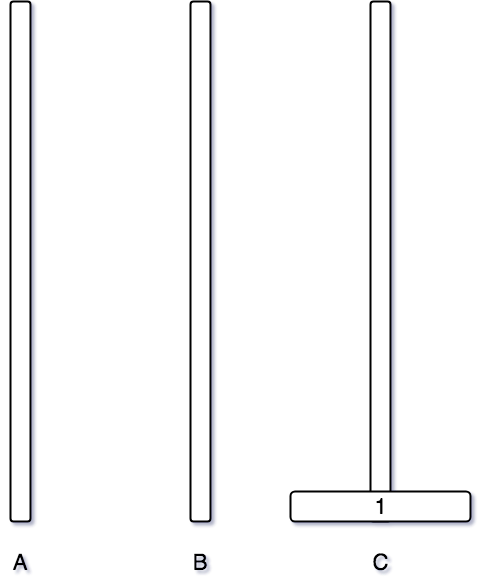
그럼 하나를 더 추가해서 A 기둥에 하나의 더 원판을 추가해서 옮겨보도록 하겠다.

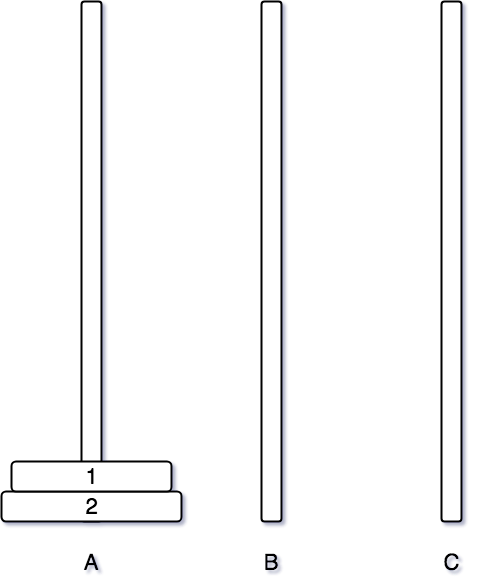
일단 먼저 2번 원판을 C 기둥으로 옮기기 위해서는 먼저 위에 쌓여 있는 1번 원판을 먼저 옮겨야 한다. 그래서 1번 원판을 B 기둥으로 먼저 옮겨둔다.

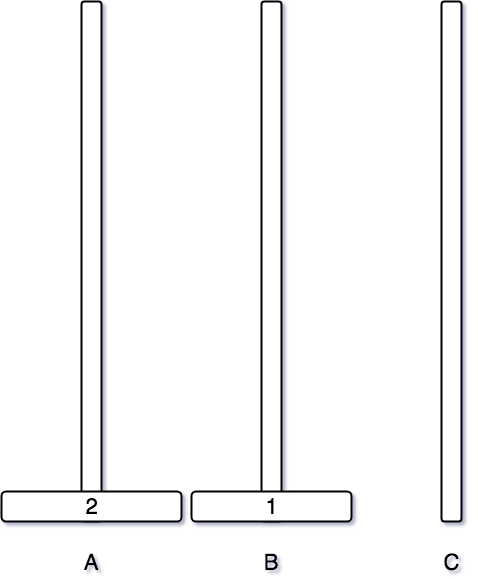
그 후에 목표인 2번 원판을 C 기둥으로 옮기면 된다.

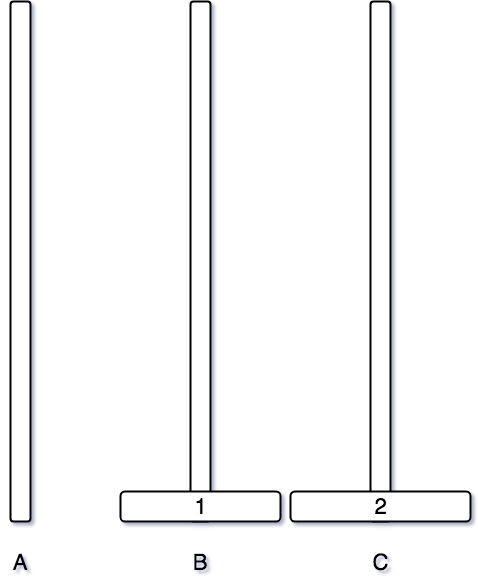
마지막으로 2번 원판 위에 1번 원판을 옮겨주면 된다.

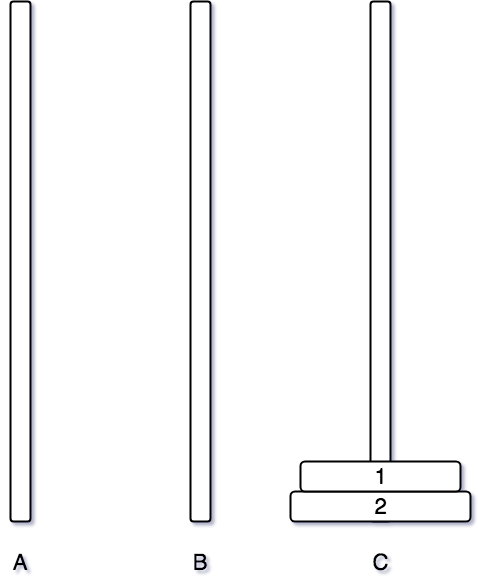
2개일때도 마찬가지로 어렵지 않게 풀 수 있다.

그럼 원판을 하나더 추가해서 총 3개의 원판을 이동시켜보겠다.

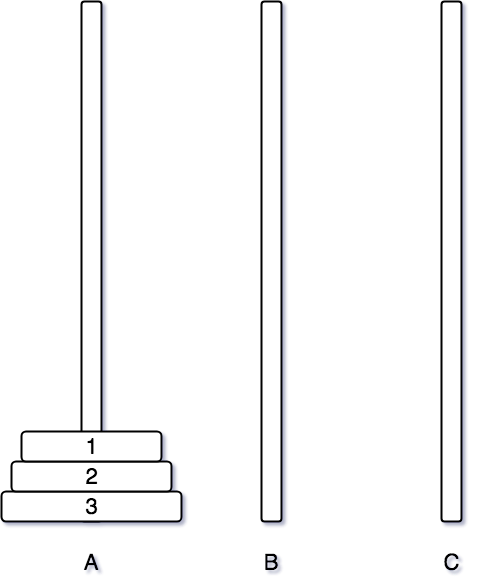
일단 먼저 1번 원판을 먼저 C 기둥으로 이동시킨다. 2개의 원판을 이동시킬 때는 1번 원판을 B 기둥으로 먼저 이동시켰는데, 3개의 원판을 이동시킬때는 C 기둥으로 옮겨놓았다는 것을 기억해야한다.

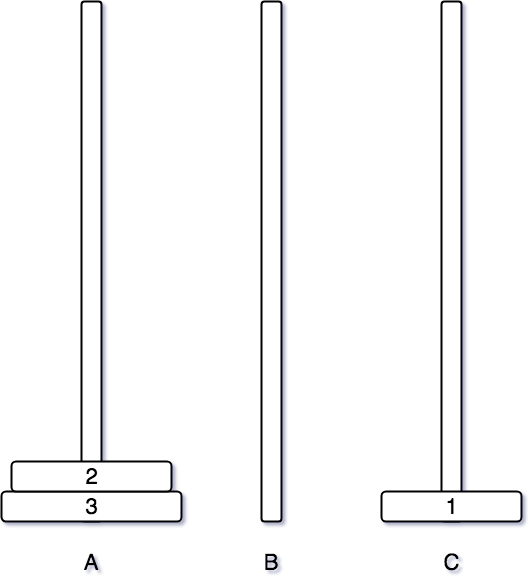
1번 원판을 옮기면 그 다음은 2번 원판을 옮길 차례다. 2번 원판은 비어있는 B 기둥으로 이동시킨다.

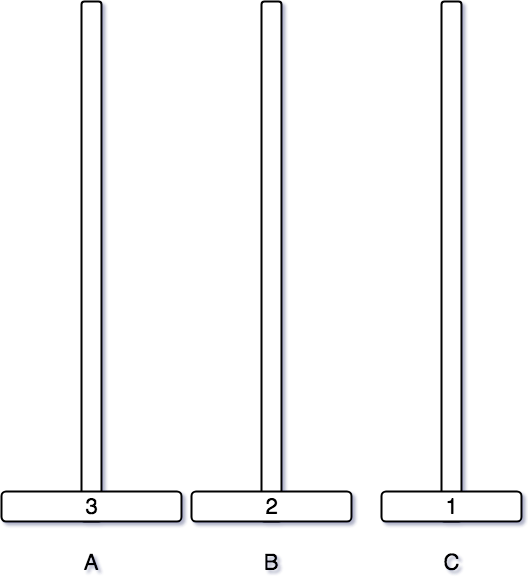
그 후에는 3번 원판이 마지막으로 옮겨질 C 기둥을 비워줘야 한다. 현재 C 기둥에 있는 1번 원판을 2번 원판이 있는 B 기둥으로 이동시킨다.

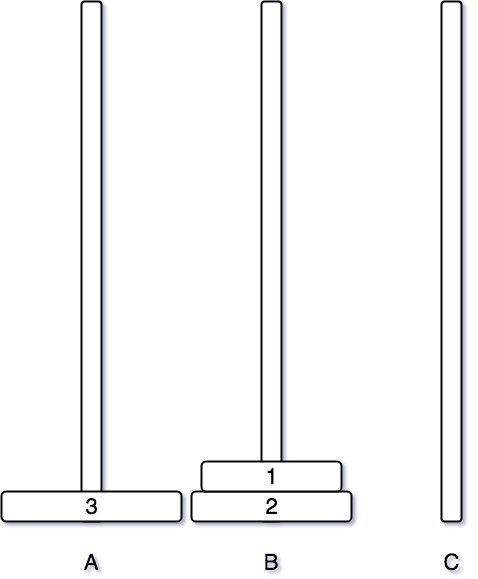
그 후 3번 원판을 우리가 목표했던 C 기둥으로 이동시킨다.

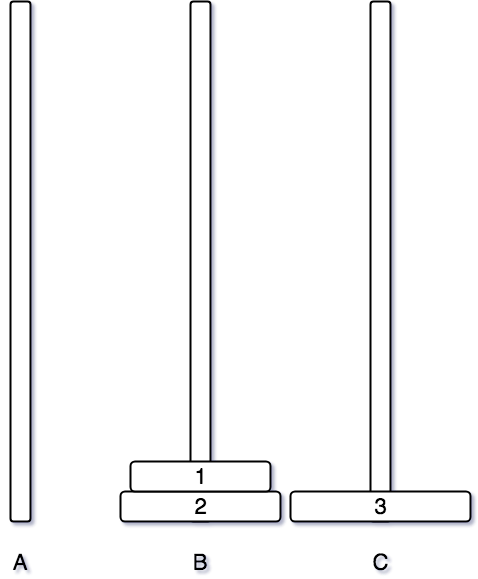
일단 우리가 목표하는 C 기둥으로 마지막 원판을 이동시켰다. 그 후에는 앞에서 했던 방법과 동일하게 A 기둥을 이용하여 1번 원판과 2번 원판을 순서대로 C 기둥으로 이동시켜주면 된다.

먼저 1번 원판을 A 기둥으로 옮겨준다.

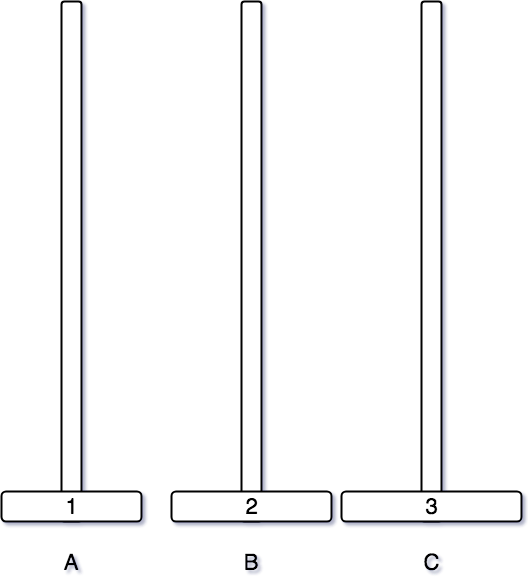
그 후, 2번 원판을 C 기둥으로 이동시켜준다.

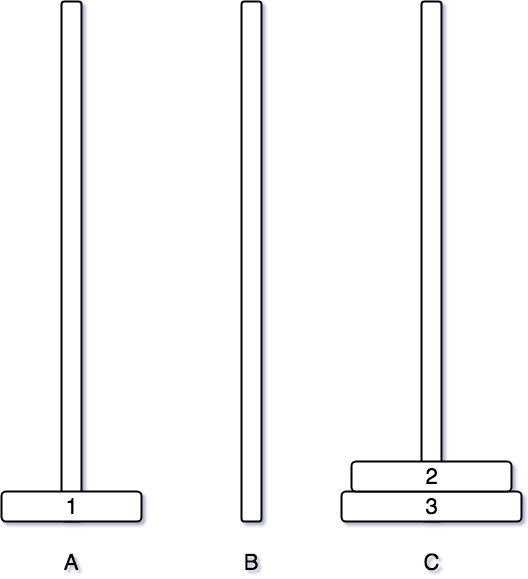
마지막으로 1번 원판을 C 기둥으로 옮겨주면 된다.

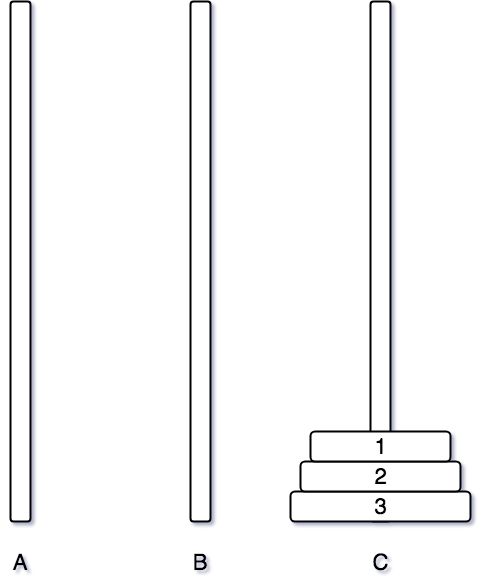
여기까지만 해도 충분히 쉽다. 원판이 하나더 추가되었을 때부터 많은 어려움을 느낄 수 있다.

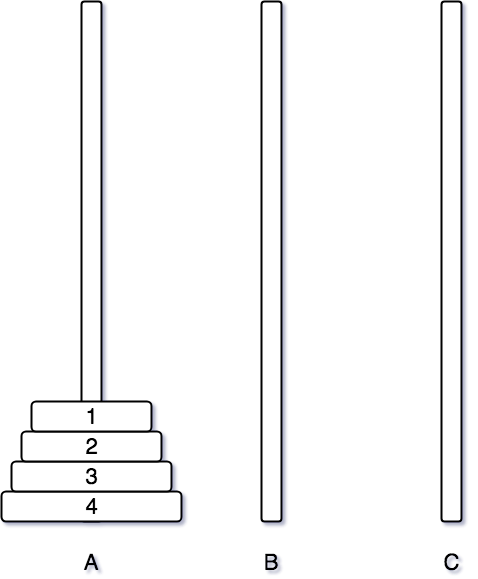
먼저 1번 원판을 B 기둥으로 이동시킨다.

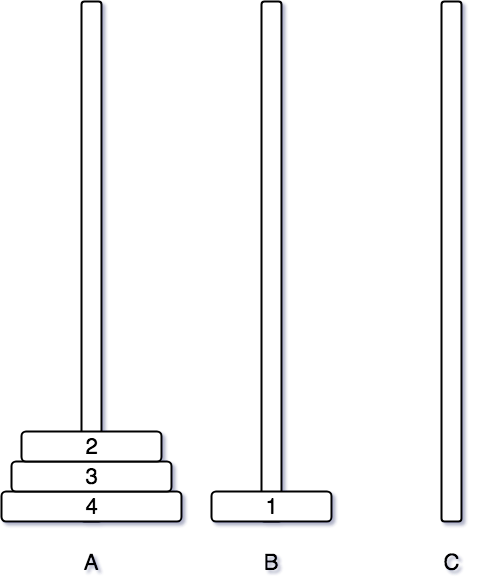
1번 원판을 이동시킨 후에는 2번 원판을 C 기둥으로 이동시킨다.

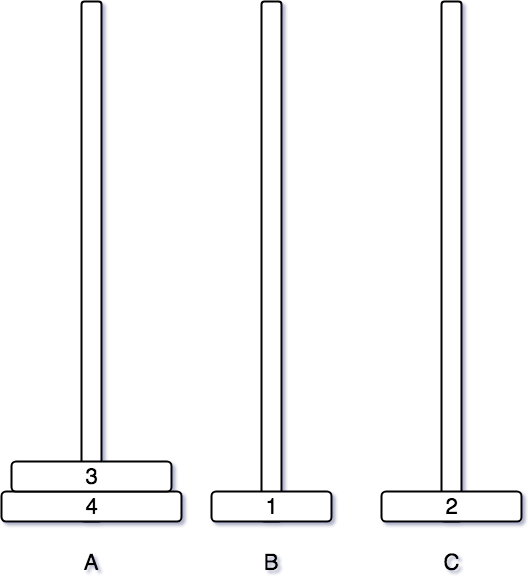
2번 원판까지 옮긴후에는 앞에서 3개의 원판을 옮길 때와 마찬가지로 1번을 2번 위로 옮긴다.

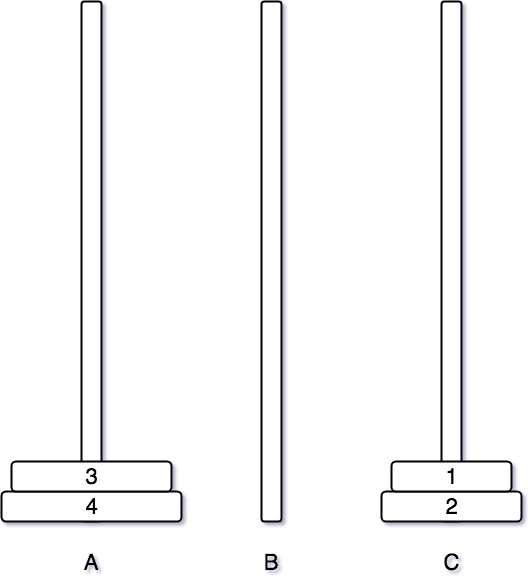
그 후 비어있는 B 기둥으로 3번 원판을 옮긴다.

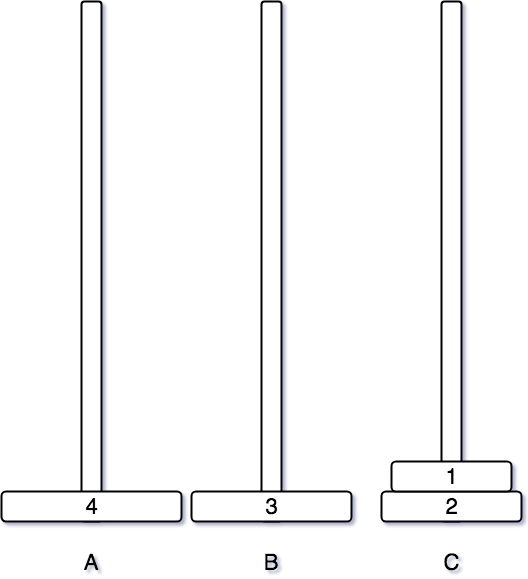
3번까지의 원판을 옮기는 데까지는 이전 3개의 원판과 동일하다. 1번 원판과 2번 원판을 을 A 기둥을 이용하여 순서대로 B 기둥으로 옮겨준다.

앞과 동일하게 먼저 1번 원판을 A 기둥으로 옮긴다.

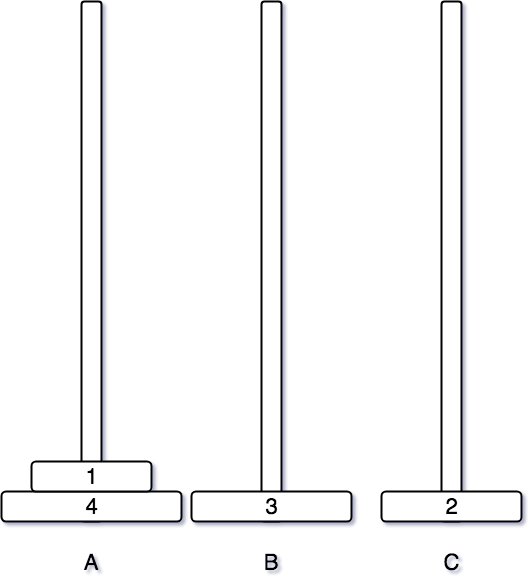
옮겨진 후에는 2번 원판과 1번 원판을 순서대로 B 기둥으로 옮긴다.

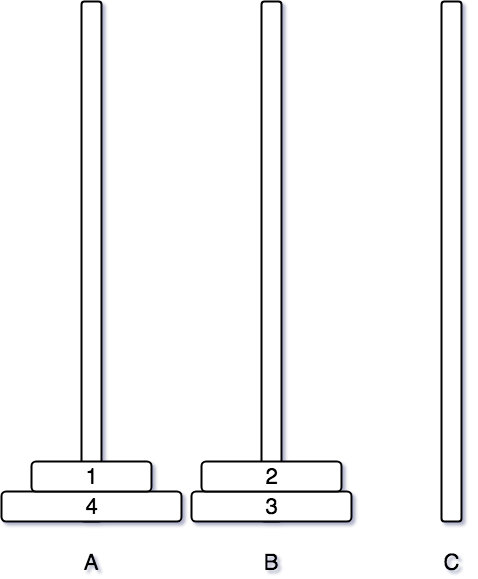
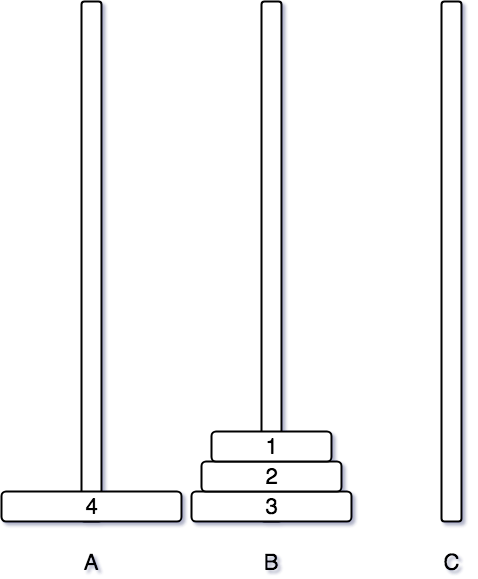
그 후에는 먼저 A 기둥에 있는 4번 원판을 비어있는 C 기둥으로 이동시킨다.

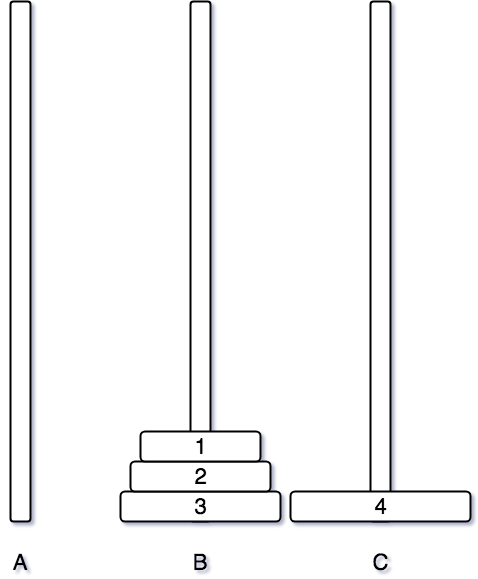
옮긴 후, 1번 원판을 C 기둥으로 2번 원판을 A 기둥으로 이동시킨다.

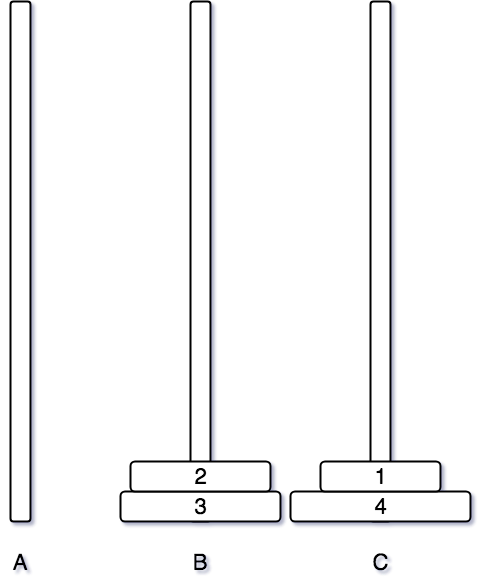
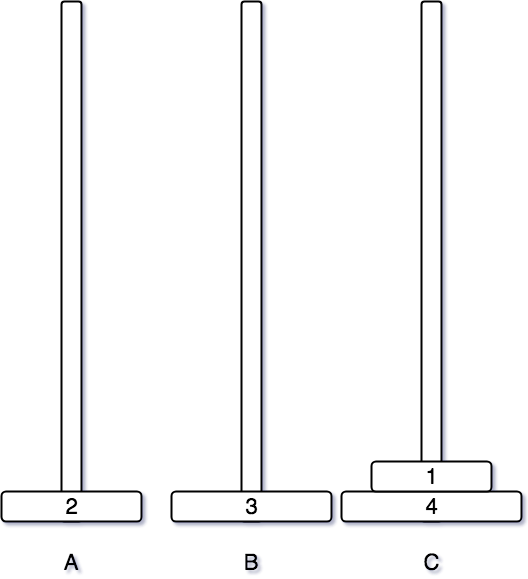
그 후, A 기둥과 B 기둥을 이용하여 순차적으로 원판을 쌓아나간다.

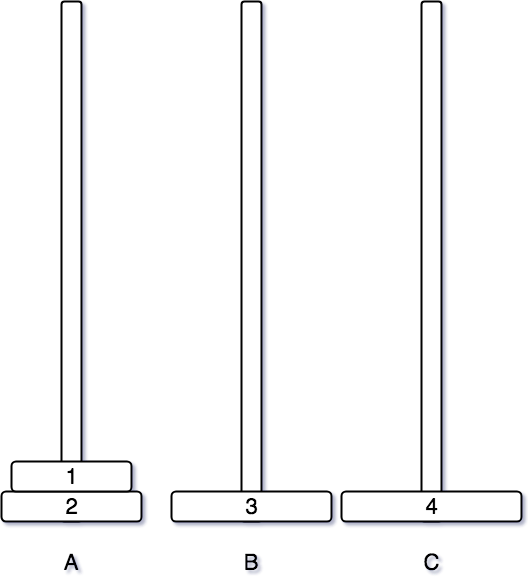
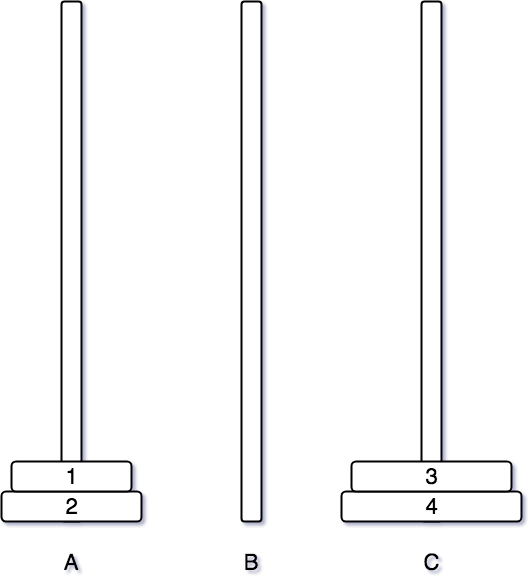
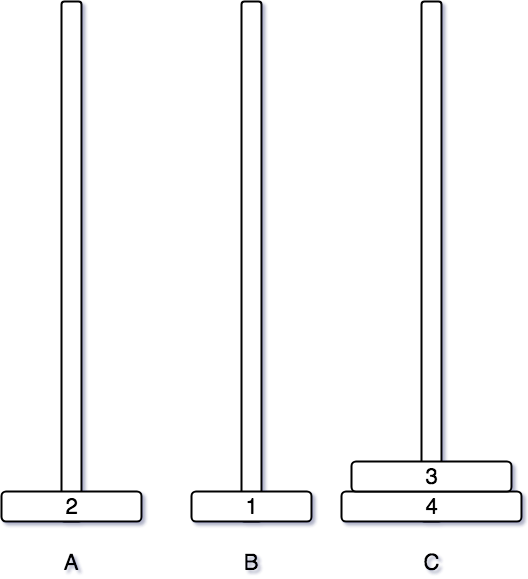
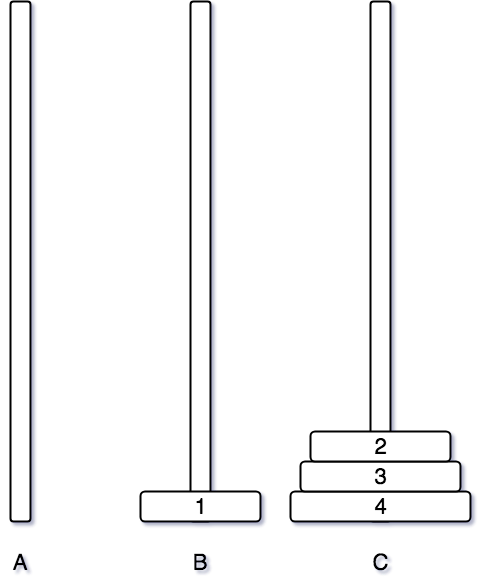
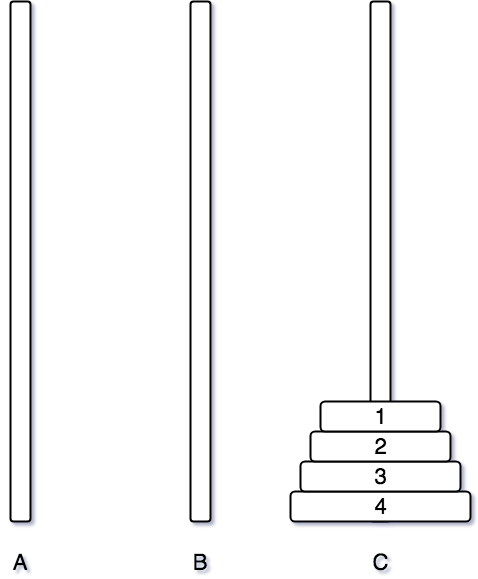
여기까지 그림으로 먼저 하노이 탑 알고리즘 옮기는 것을 봤다.

하노이 탑 연관성 찾기

위에서 그림으로 기둥으로 옮기는 것을 확인했다. 이제 코드로 풀이하기 위해 먼저 연관성을 찾아보자.

원판이 1개만 있었을 때

1. A 기둥에 있는 원판을 C 기둥으로 이동한다.

원판이 2개만 있었을 때

1. A 기둥에 있는 원판을 B 기둥으로 이동한다.
2. A 기둥에 있는 원판을 C 기둥으로 이동한다.
3. B 기둥에 있는 원판을 C 기둥으로 이동한다.

원판이 3개만 있었을 때

1. A 기둥에 있는 원판을 C 기둥으로 이동한다.
2. A 기둥에 있는 원판을 B 기둥으로 이동한다.
3. C 기둥에 있는 원판을 B 기둥으로 이동한다.
4. A 기둥에 있는 원판을 C 기둥으로 이동한다.
5. B 기둥에 있는 원판을 A 기둥으로 이동한다.
6. B 기둥에 있는 원판을 C 기둥으로 이동한다.
7. A 기둥에 있는 원판을 C 기둥으로 이동한다.

원판이 4개만 있었을 때

1. A 기둥에 있는 원판을 B 기둥으로 이동한다.
2. A 기둥에 있는 원판을 C 기둥으로 이동한다.
3. B 기둥에 있는 원판을 C 기둥으로 이동한다.
4. A 기둥에 있는 원판을 B 기둥으로 이동한다.
5. C 기둥에 있는 원판을 A 기둥으로 이동한다.
6. C 기둥에 있는 원판을 B 기둥으로 이동한다.
7. A 기둥에 있는 원판을 C 기둥으로 이동한다.
8. B 기둥에 있는 원판을 C 기둥으로 이동한다.
9. B 기둥에 있는 원판을 A 기둥으로 이동한다.
10. C 기둥에 있는 원판을 A 기둥으로 이동한다.
11. B 기둥에 있는 원판을 C 기둥으로 이동한다.
12. A 기둥에 있는 원판을 B 기둥으로 이동한다.
13. A 기둥에 있는 원판을 C 기둥으로 이동한다.
14. B 기둥에 있는 원판을 C 기둥으로 이동한다.

그렇다면 n 개의 원판을 이동하는 경우는 어떻게 될까?

원판이 n개 있었을 때

1. A 기둥에 있는 n-1 번째 원판을 B 기둥으로 이동한다.
2. A 기둥에 있는 n 번째 원판을 C 기둥으로 이동한다.
3. B 기둥에 있는 n-1 번째 원판을 C 기둥으로 이동한다.

위의 내용을 종합해보건데, 하노의 알고리즘의 계산은 다음과 같다.

1. n-1 개의 원반은 A 기둥에서부터 B 기둥으로 옮기는 데 Hanoi(n-1) 이 걸린다.
2. n 개의 원반은 A 기둥에서부터 C 기둥으로 옮기는 데 Hanoi(1) 이 걸린다. (Hanoi(1) 은 한번만 이동하면 되므로 1 로 계산한다.)
3. n-1 개의 원반은 다시 B 기둥에서부터 C 기둥으로 옮기는 Hanoi(n-1) 이 걸린다.

그러므로 총 계산해보면 알고리즘의 수식은 2Hanoi(n-1) + 1 이다.

아래의 코드는 프로그래머스(programmers)에 나오는 하노이 탑 알고리즘에 대한 해답이다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

function solution(n) {
  const answer = [];

  function hanoi (n, from, to) {
    const by = 6-from-to;

    if (n === 1) {
      answer.push([from, to]);
    } else {
      hanoi(n-1, from, by);
      answer.push([from, to]);
      hanoi(n-1, by, to);
    }
  }
  hanoi(n, 1, 3);

  return answer;
}

위의 에제의 경우 재귀함수를 이용하여 풀었지만 이에 대한 문제점으로는 재귀함수의 고질점인 문제, 스택오버플로우(stack flow) 에 대한 문제가 해결 되지 않았다. 이후 스택을 이용하여 이에 대한 해결 방법을 찾도록 하겠다.
이상으로 하노이 알고리즘에 대한 포스팅을 마치겠다.

아래는 위에서 이야기한 재귀함수의 고질적인 문제를 해결하기 위해 비재귀 방식인 스택을 이용하여 문제를 풀어보겠다. 많은 블로그에서 재귀함수에 대해서 많이 다루고 있으나, 비재귀방식으로 하노이 알고리즘을 푸는 글들이 없어서 소스를 첨부한다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

function solution (n) {
  const result = []; 
  function hanoi (n, from, to) {
    const arr = [];
    let temp = 1;
    let by = 6-from-to;
    while (temp > 0) {
      while (n >1) {
        arr.push(to);
        arr.push(by);
        arr.push(from);
        arr.push(n);
        n--;
        arr.push(to);
        to = by;
        by = arr.pop();
      }
      result.push([from, to]);
      if (arr.length -1 > 0) {
        n = arr.pop();
        from = arr.pop();
        by = arr.pop();
        to = arr.pop();
        result.push([from, to]);
        n --;
        arr.push(from);
        from = by;
        by = arr.pop();
      } else {
        temp = 0;
      }
    }
  }
  hanoi (n, 1, 3);
  return result
}

출처

• programmers 알고리즘 사이트
• [알고리즘 도감 - 이시다 모리테루, 미야자키 쇼이치 저자]